求め方1:微笑の範囲を考える方法 求め方2:球体の体積を用いる方法 求め方1:微小の範囲を考える方法 考え方 青い部分の面積 を考える. 幅は 、長さは なので, より微小な角度を考える 球全体で積分する 計算 求め方2:球の体積を用いる方法 考え方球 ボール 体積計算 公式 求め方 計算方法 直径 半径 自動 円周率 volume 中1数学「球の表面積と体積の求め方」練習問題有についてまとめています。 球の表面積と体積は、入試や定期テストでもよく出題される単元です。 しかしながら、テスト本番で、公式を思い出せなかったということも少なくないです。 何度も問題を解い

球の表面積と体積の求め方 苦手な数学を簡単に
球 体積 求め方
球 体積 求め方-例題2:半径が 2 c m の半球の表面積を計算してみましょう。 公式を使うと、 3 × π × 2 × 2 = 12 π c m 2 と計算できます。 円周率 π はおおよそ 314 なので、半球の体積はおおよそ、 12 × 314 = 3768 c m 3 となります。313 体積の計算 次 314 曲面積 上 3 多重積分 前 312 演習問題 ~ 多重積分の積分変数の変換 3 13 体積の計算 例 3 63 (球の体積) 半径 の球の体積は である. これを多重積分で求める.




球の表面積の公式と球の体積の公式 中学生の数学 要点 Yattoke 小 中学生の学習サイト
球を1つの平面で切り取った部分である球欠について考えます。凸レンズの体積を求める際にも利用できます。 Ⅰ 球欠と球冠とは? Ⅱ 球欠の体積 Ⅲ 球冠の面積 Ⅰ 球欠と球冠とは? 言葉とし球の体積 110 /79件 表示件数 5 10 30 50 100 0 1 26 男 / 歳代 / 高校・専門・大学生・大学院生 / 役に立った / 使用目的 前立腺はくるみ大といわれるが、一般的なくるみのサイズで半径15cmで計算してみたら14強になり、前立腺肥大の閾値が>mL 《球の体積の求め方》 球の直径が6cmなので半径は3cm。 求める球の体積を V 、半径を r とすると V = 4 3πr³ より V = 4 3π × 33 = 4 3π × 27 = 36π
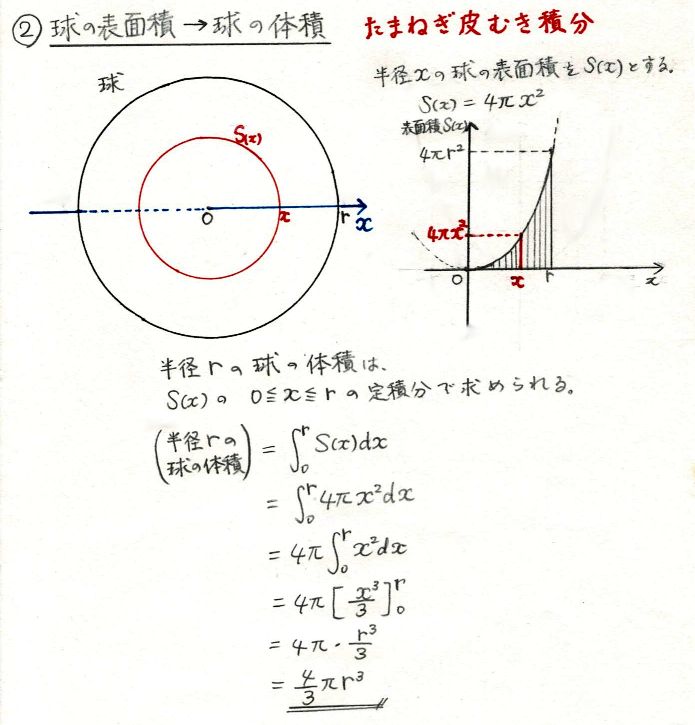
球の体積は、中心から表面までの距離 (常に一定)を半径rとすると、 4/3 * π * r3 このような球殻を t = 0 から t = r まで足し合わせたものが半径 r の球であり、体積は \displaystyle \frac {4} {3} \pi r^3 である。 よって、 \Delta t を限りなく 0 に近づけると、球殻の体積について以下の式が成り立つ。 \displaystyle \int_0^r S (t) \, dt = \frac {4} {3} \pi r^3球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。
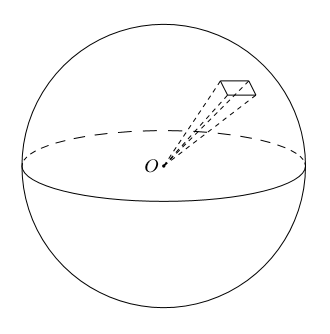
①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の球の半径を入力 r = 10 球の体積 V = 球の表面積 S = ここでは半径「10」の球の体積と表面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください。 C言語のサンプルプログラム集 中学数学球の表面積の求め方の公式を1発で覚える方法 球の表面積の求め方の公式はおぼえにくい?? こんにちは!この記事をかいているKenだよ。豚肉を今日もいためたね。 球の表面積の求め方には公式があるんだ。 球の半径をrとすると、その表面積
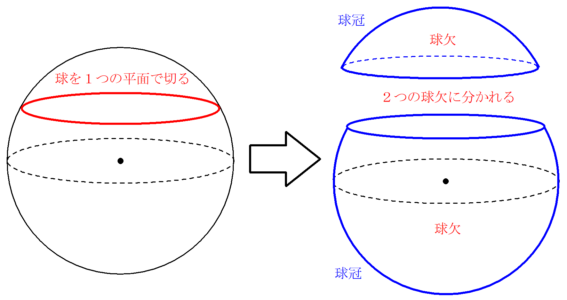



球欠と球冠 Fukusukeの数学めも




球の表面積の公式について みたにっき はてな
球の体積の求め方の問題が解けていなかったので、驚きました。 確かに、球の体積の求めかたの公式、とっても覚えにくいですよね。 きょうは、その覚えにくい球の体積について、丸暗記ではない方法をお伝えします。 まず、こちらの図です。 (1B)微小面積(体積)を幾何学的に計算して積分する方法 求めたい面積 S は、変数を x, y とすると、 S = ∫ ∫ d x d y として微小面積について x と y について足し合わせればよい。 薄い球殻の体積を求めたい。 球殻は、中心を同じくする大きい球と小さい球とに挟まれた領域と言えるので、大きい球の半径を r dr 、小さい球の半径を r とすると、体積 V は以下の式で表せる。 V = 4 3π(r dr)3 − 4 3πr3




中1数学 球の表面積と体積の定期テスト過去問分析問題 Atstudier



中学数学 球の体積の何で 数樂管理人のブログ
球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半球の体積の解説 球の体積は 4/3×円周率×半径×半径×半径=体積 で求めることができます。円周率をπ、半径をr、体積をVとすると、 V=4/3πr 3 となります。 球の体積を求体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱(管) 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方




球冠 Wikipedia



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス
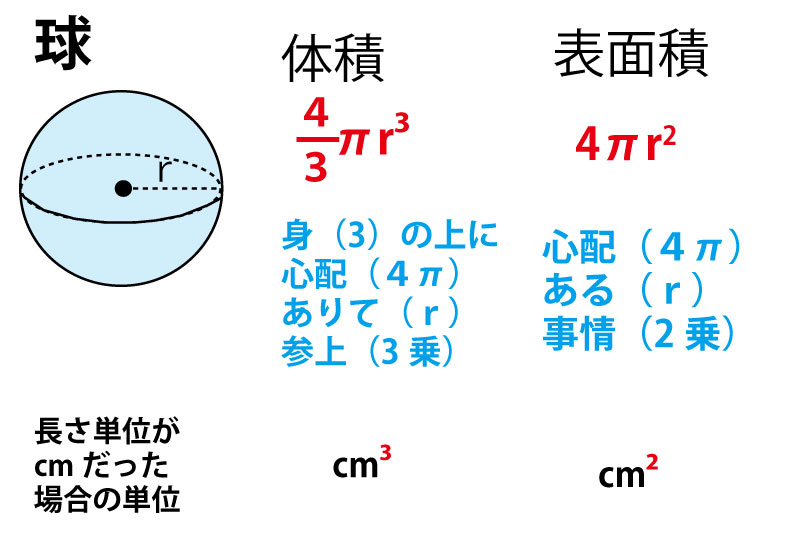
人類はどうやって球の体積を求めたのか 1、アルキメデスは球の体積をどうやって見つけたの? T:球の体積は半径をrとすると、4/3・π・r 3 で求めることができるんです。 覚え方は、『3分で忘れる心配あーるの参上。体積 = たて × 横 × 高さ一部が欠けた球の体積 こういうサイトを探していました。 助かりました。 液体接触角の滴定量計測。 今まで表計算ソフトを使って手入力計算していましたが、偶然こちらのサイトを見つけました。 もっと早く見つければよかったです。 超音波




球の表面積の求め方 公式と計算例
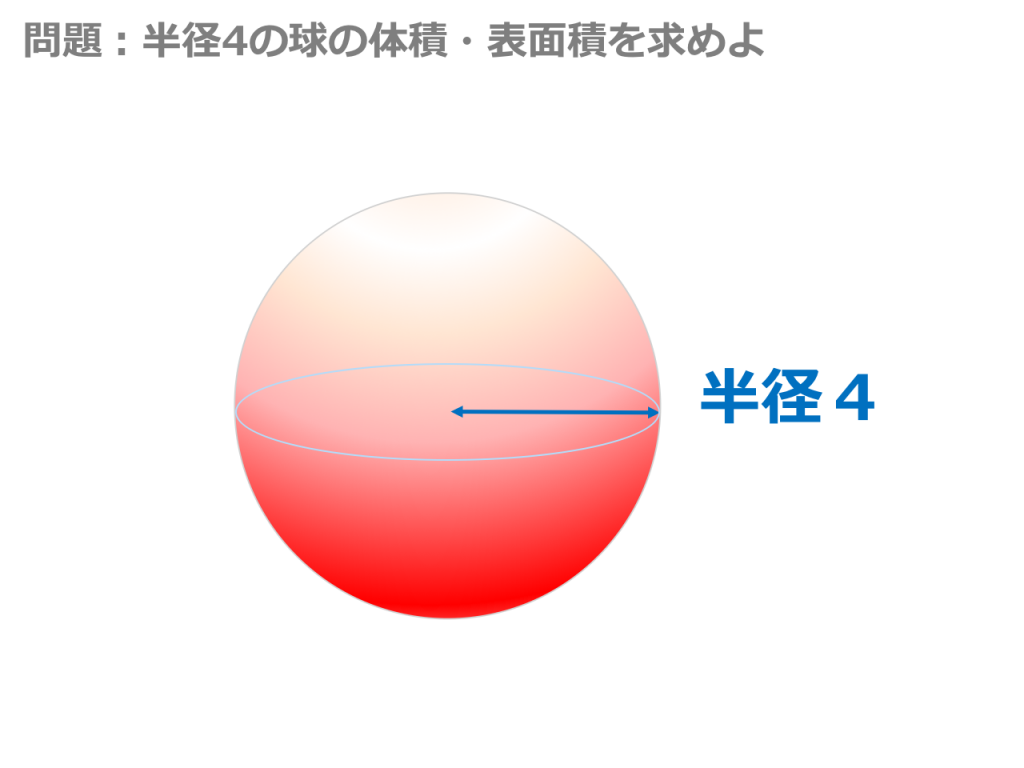



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ
下記の記事で、\(n\)次元空間の半径\(R\)の球の体積というのを求めました。 前回の記事はこちら n次元空間における半径Rの球の体積 ↑結果はこちらです。 せっかくなので、2次元、3次元、4次元、5次元の球の体積 球の体積 最後に、球の体積問題を解説します。 球の体積 \(V\) は $$ V= \frac{4}{3} \pi r^3 $$ という公式で求まります。 この公式がどうやって出てくるかを説明するには高校数学の積分が必要なんで、中学生はもう覚えてしまいましょう。 r r の球の表面積は S=4\pi r^2,\ S = 4πr2, 球の体積は V=\dfrac {4} {3}\pi r^3 V = 34 πr3 である。



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




球の表面積の公式と球の体積の公式 中学生の数学 要点 Yattoke 小 中学生の学習サイト
高次元超球の体積の求め方 公開21年2月23日 工学 / 数学 ガンマ関数 / 特殊関数 / 積分 / 超球 / 高次元 この記事では一般 d d 次元超球の体積について,その求め方をご紹介します。 超球の体積の求め方は幾つか知られていますが,ここでは僕が直感的に はがし方① 下図のように切り込みを入れてはがす。 横の長さ=球の一周分の長さ= 2πr 縦の長さ=球の半周分の長さ= πr 形を単純にしてだいたいの面積を求める. 面積= πr × 2πr × 1 2 = π2r2 = 314πr2 形を切り落として考えているため,実際の面積は解答 1 基本計算モードを選択。 2 球の体積の式4π× () 3 /3を入力。 3 答えを求める。 これより地球の体積は約x10 12 立方kmであることがわかる




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




球の体積の求め方を教えていただけませんか よろしくお願いしますm M Clear
中学生でもおぼえられる「球の体積の求め方」 を解説していくよ。 球の体積の公式を忘れちゃったときに参考にしてみて。 球の体積の公式を1発で覚える方法 「球の体積の公式」を暗記する方法を伝授しよう。 3分の4 × 円周率 × 半径の三乗21 球の体積(アルキメデスの求積) ここでは,アルキメデスによる球の体積の求め方について述べる. 力のモーメントを用います.力のモーメントといっても棹秤(さおばかり)の性質です. すなわち,棹ばかりの重さを無視すれば右図でつり合いがとれていれば




球の体積 表面積 無料で使える中学学習プリント




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球の表面積と体積の公式 数学fun
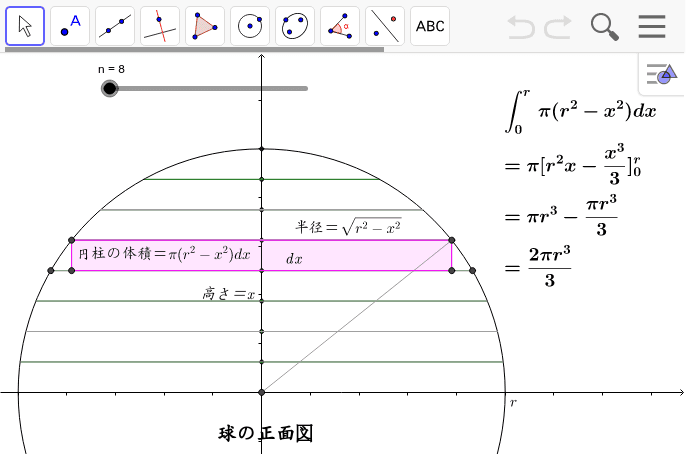



球の体積の積分 Geogebra




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ




球の体積の公式を積分を使わず導く 中受でも出るかも 兄中学生活




球の体積 表面積 無料で使える中学学習プリント




中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




球の体積と表面積 数学i フリー教材開発コミュニティ Ftext




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




2次元 3次元 4次元 5次元 高次元 の球の体積 宇宙に入ったカマキリ



研究




球の体積と表面積 Youtube



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ
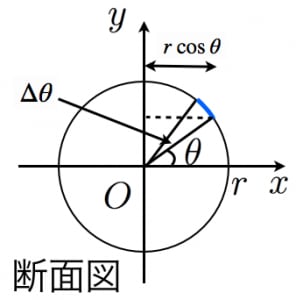



球の体積と表面積を積分で証明 高校数学の美しい物語




球の体積公式の微分が表面積になっている理由 Youtube




球体の体積 中学生に分かるように真剣に考えてみた うちーノート




球に関する公式 理数系無料オンライン学習 Kori



1




中1 数学 中1 84 球について Youtube




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館




中1数学 球 練習編 映像授業のtry It トライイット




球の表面積と体積の公式 数学fun



1



U9j580gf8iba369ji2w Xyz P 296




球の表面積と体積の求め方 苦手な数学を簡単に



1




角錐 円錐の体積と表面積の公式 数学fun




球の体積と表面積を積分で証明 高校数学の美しい物語




面積 体積 計算ツール 福井鋲螺株式会社 冷間鍛造 冷間圧造 ヘッダー加工の専門メーカー リベット 特殊形状パーツおよび省力機器の製造 販売



球の体積の求め方とその証明 高等学校で学ぶ積分の知識が必要




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
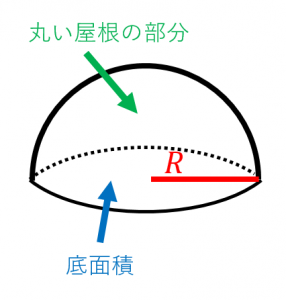



半球の体積と表面積を計算する 具体例で学ぶ数学




球の表面積と体積の公式 数学fun
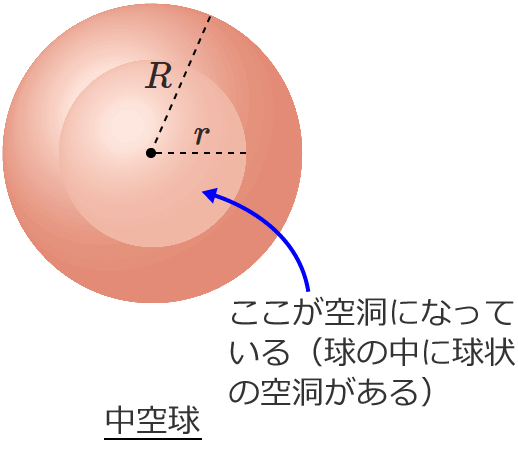



立体の体積を求める公式



1 この球の体積と円柱の体積の比を求めなさい 2 この球の表面積と円柱の Yahoo 知恵袋



球の体積 簡単に計算できる電卓サイト




球表面積 なぜ 勉強しよう數學 Ptnoe




Excel エクセルで球の体積と表面積を計算する方法 白丸くん
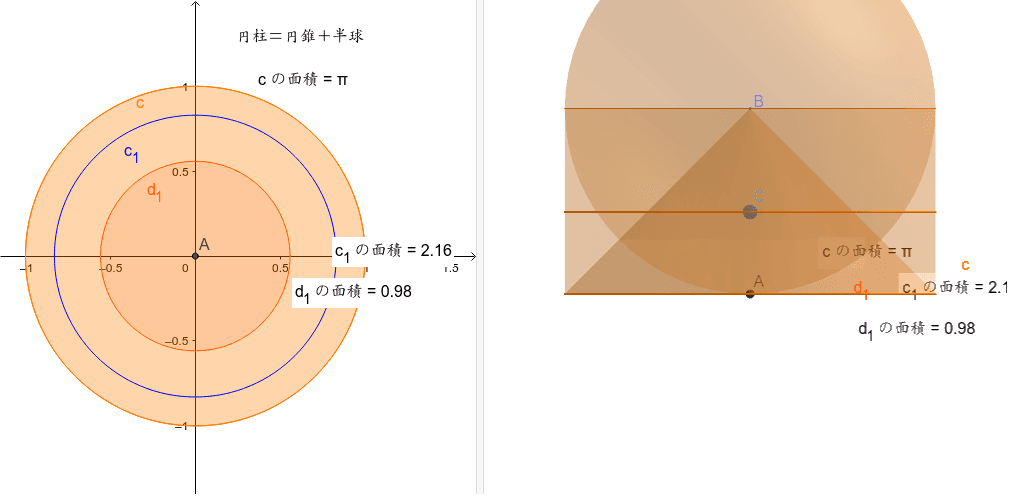



球の体積の求め方 Geogebra
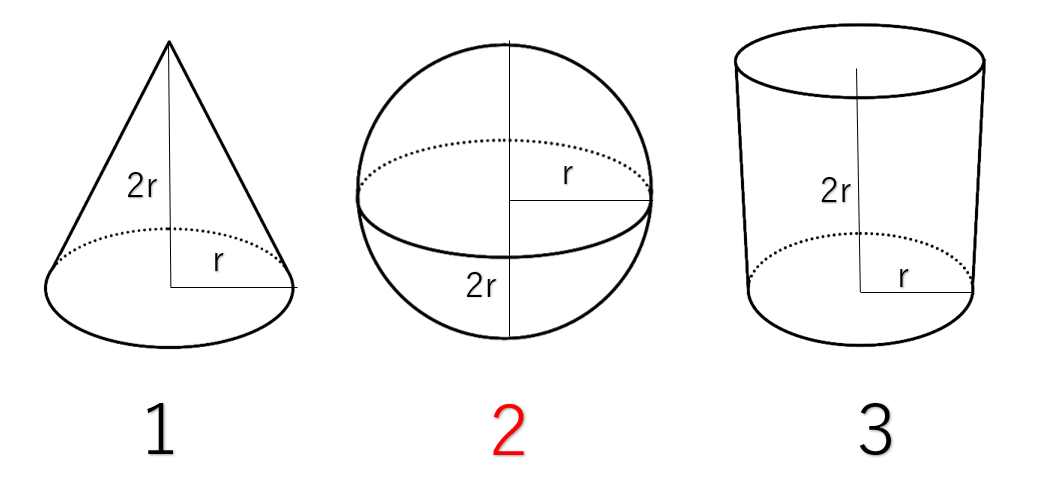



中1 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾




初等幾何 球の表面積を求める 大人が学び直す数学




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ
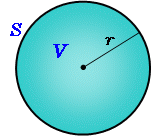



球の体積 高精度計算サイト



1




球の体積の求め方 公式の覚え方と計算方法まとめ 中学数学 理科の学習まとめサイト




球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube




球の体積の求め方でなぜ3分の4が出てくるのかわかりません 中1でもわかるように説明お Clear



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




球の体積と表面積 公式と計算問題と証明 Irohabook




Mathematics 球の体積と表面積を求める公式 働きアリ



Studydoctor球の表面積や体積の公式と求め方 中学1年数学 Studydoctor




中1 数学 6 5 球の体積 表面積 Youtube



球の表面積の公式の求め方
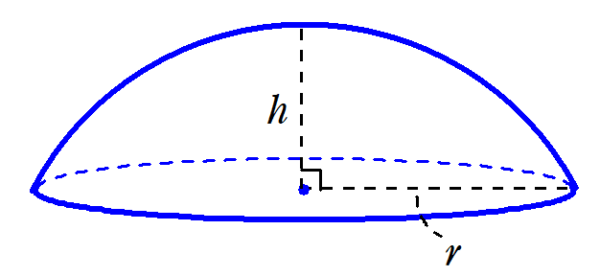



球欠と球冠 Fukusukeの数学めも



球の表面積の公式の求め方



至急 球を4等分したものの体積と表面積の求め方をを教えてください Yahoo 知恵袋




球の表面積と体積の公式 数学fun




球の体積の求め方 感じる科学 味わう数学




この答えは2p になるんですが この球の体積の求め方とどうやったらこの答えに Clear



大学入試問題




球の表面積 体積 身勝手な主張




中1数学 球 例題編 映像授業のtry It トライイット



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




中1 中一数学 球の表面積と体積 中学生 数学のノート Clear




モヤモヤからワクワクへ 乱数 モンテカルロ法 を使って球の体積を求めてみよう Pythonを使う




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



立体 の 表面積 求め 方




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




中1数学 空間図形 球の体積の求め方 Youtube



19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
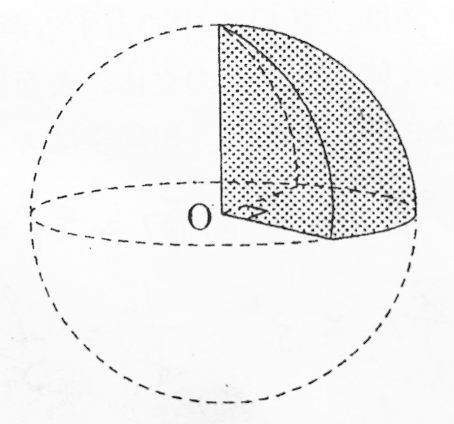



球の問題 苦手な数学を簡単に




薄い球殻の体積と直方体の体積 の宇宙




中学数学 空間図形 体積の問題のコツ




体積とは コトバンク




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく




球の体積と表面積 Jsciencer




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題




Www Yuulinux Tokyo Contents Wp Content Uploads




半球の体積と表面積を計算する 具体例で学ぶ数学




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



球の表面積と体積 計算ドリル 問題集 数学fun




中1 中1数学 球の体積と表面積 中学生 数学のノート Clear



0 件のコメント:
コメントを投稿