
有効数字二桁で表すとどっちが合ってますか 有効数字二桁で表すとどっ 数学 教えて Goo
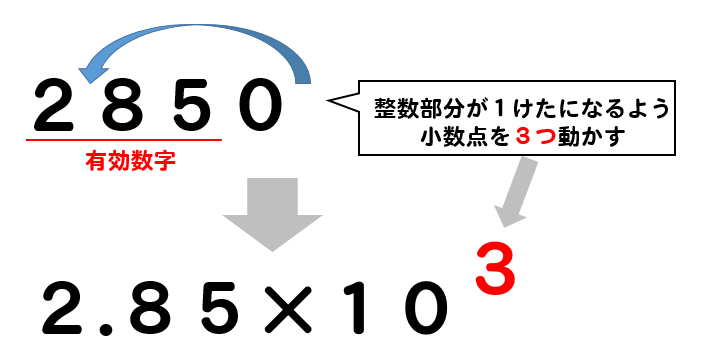
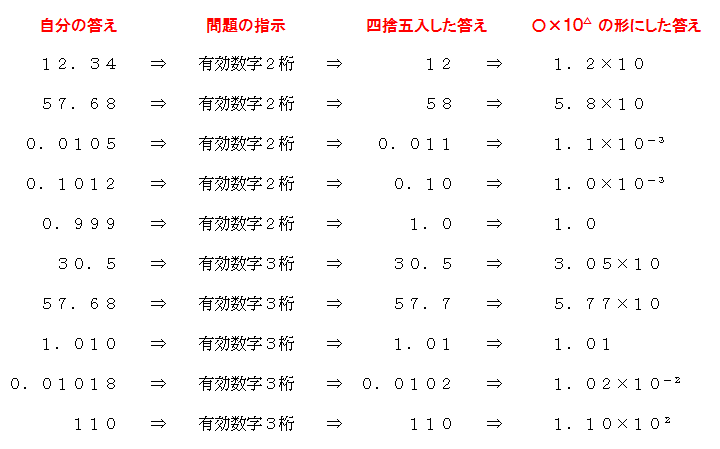
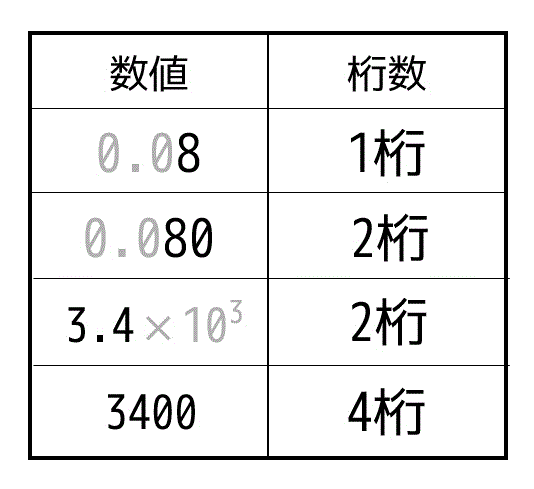
有効数字の考え方 (改訂25) 数値計算の結果は不確実な値を含む 有効数字2桁なら 1 → 10 03 → 030 1 → 12×102 598 → 60×102 有効数字の意味 理科では数学と違い,有効数字というルールがある。その1 有効数字の最初の数字は、0じゃない一番左側の数字のことを指しています。例)では,有効数字は「138」の 3桁であり、「1」より上(左側にある)の「0」は有効数字とは言いません。 その2 二つの有効数字の間にあるゼロは有効数字です。
有効 数字 数学
有効 数字 数学-有効数字とは値として意味のある小数のことです。有効数字の詳細は下記をご覧ください。 有効数字とは?近日公開予定 ただし100、1000を、下記のように小数で表します。このとき100は有効数字3桁、1000は有効数字4桁です。 100 ⇒ 100×10 2 ⇒ 有効数字3桁有効数字 近似値を表す数のうち、信頼できる数字を 有効数字 と呼び、以下のように表す。 (整数部分が1桁の少数)×(10の累乗) 例1:10gの位まで測定した7gを有効数字を用いて表せ。 有効数字は7、2となる。

資料の整理その4 近似値と有効数字 中1数学教科書第7章 14分 Web朝倉学校 数学 朝倉幹晴 船橋市議 予備校講師 年5月7日 Youtube
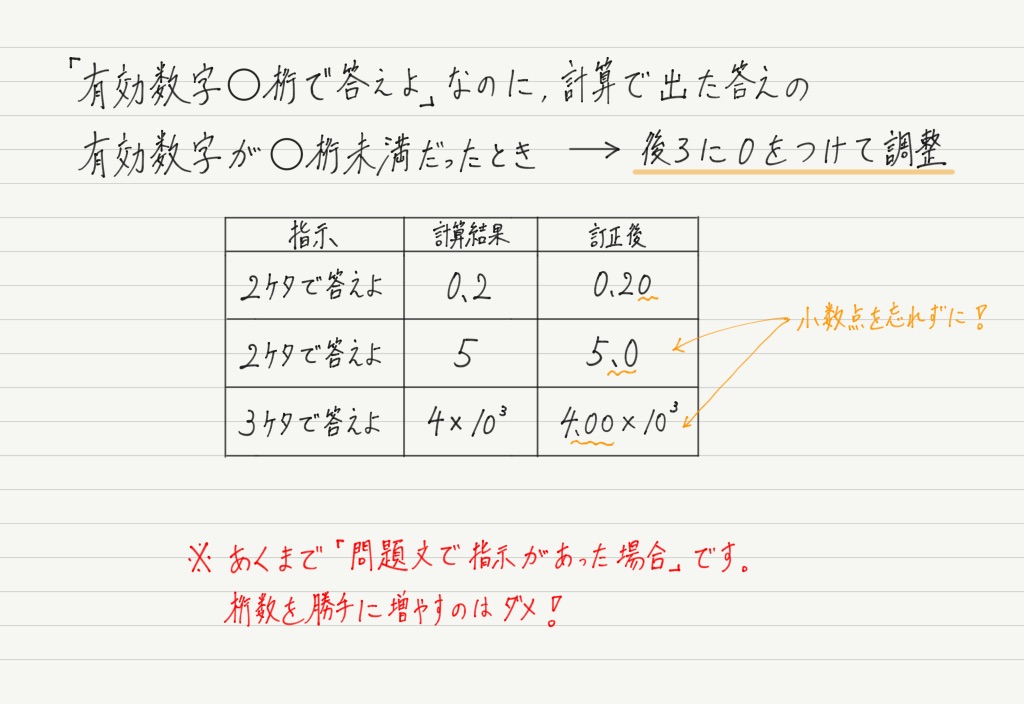
積や商の有効数字の桁数が一番小さいものと合うように四捨五入する(計算の途中で四捨五入しない!) 例えば、1234と765という測定値の積を計算しましょうか。 1234の有効数字は 4桁 765の有効数字は 3桁 なので、 積の有効数字は少ない方の3桁 に合わせ1有効数字 データで用いる数値は、デジタルにしてもアナログにしても必ず誤差があります。 まとめ センター試験 データ分析 中学1年生 中学2年生 中学3年生 問 問題 平面図形 数と式中3数学「真の値と近似値の定期テスト過去問分析問題」 近似値・誤差の練習問題です。 最近少しずつ入試でも出題され始めたところであります。 練習を重ねて習得していきましょう。 近似値・誤差 近似値と誤差真の値に近い値を近似値、近似値と
近似値を正確に:指数記法と有効数字、丸めとは何か どうも、木村( @kimu3_slime )です。 およその数(近似値)を適切に扱うことは、数学や科学において重要です。 小学校では四捨五入、中学や高校では指数記法と有効数字について学びますが、今回は有効数字の計算方法・考え方がわからん!! こんにちは、折り紙にはまっているKenです。 中1数学における難関の1つに、 有効数字の計算 というものがあります。 有効数字なんて見た目最小有効数字 測定値の内の最小有効数字に着目,他の測定値はこれより1桁多く取って計算 *1028は,四捨五入して,有効数字3桁に丸めてしまう。 計算例2 上降伏点の荷重P uy =481×10 3 N,d 0 =121mmの時,上降伏応力の計算。最小有効数字は荷重値の3桁。
有効 数字 数学のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | ||
 |  |  |
「有効 数字 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「有効 数字 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「有効 数字 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「有効 数字 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「有効 数字 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
「有効 数字 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
「有効 数字 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「有効 数字 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「有効 数字 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「有効 数字 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
「有効 数字 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
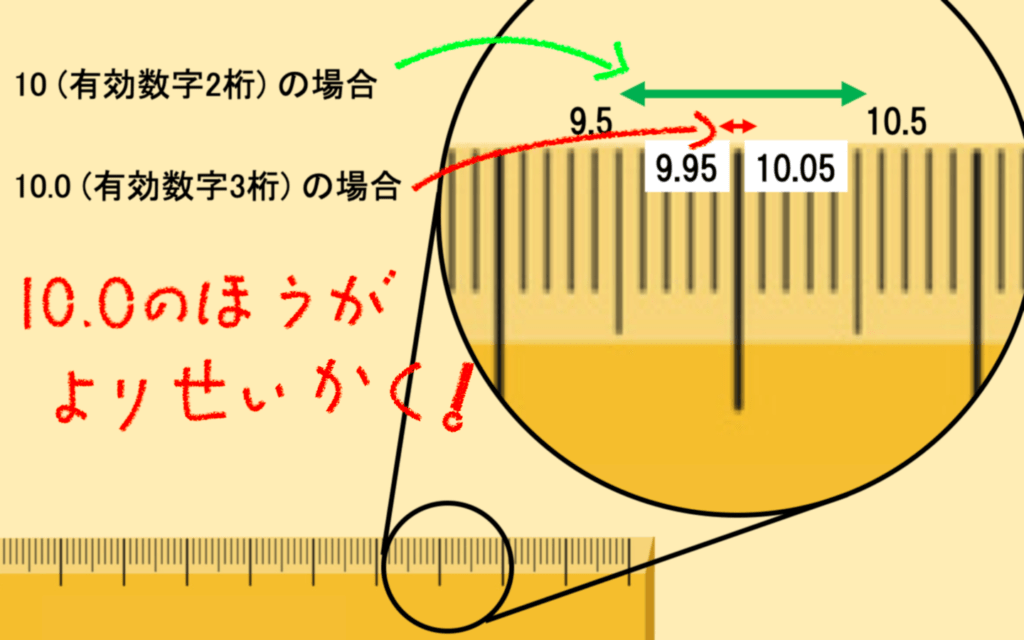
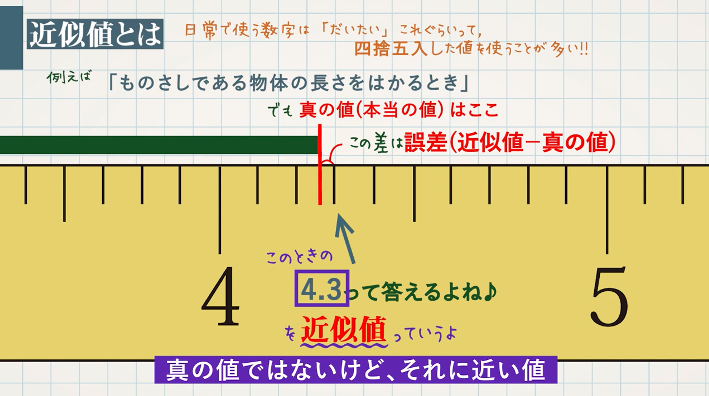
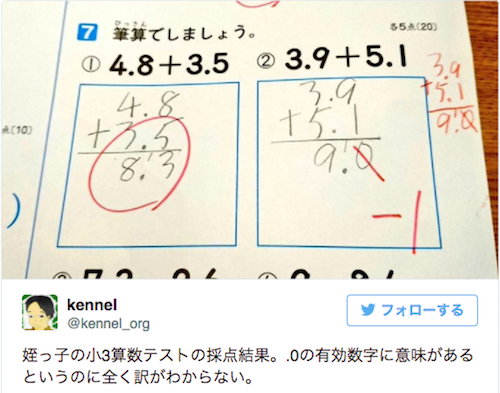
誤差と有効数字、近似値の表し方の問題です。高校の理科でも使う分野なので、教科書でしっかり意味を確認してから問題に取り組んでください。誤差とは、真の値と近似値との間にある違い、つまり、誤差=近似値-真の値です。例)測定値 505kg 真の値 502kg のとき 505kgー502kg=03kgが誤差例)100の有効数字は,1桁かもしれなし,3桁かもしれない.3桁の場合には,100 x 102 のように有効数字を明示する(規則(iii)). v) 有効数字の桁数は,単位の取り方とは無関係である. 例)117 mgの有効数字は3桁であるが,単位を変えて「 g」,「117 x 104 µg」





0 件のコメント:
コメントを投稿