
数学a 6の倍数であることの証明 オンラインプロ家庭教師 理数ゼミ
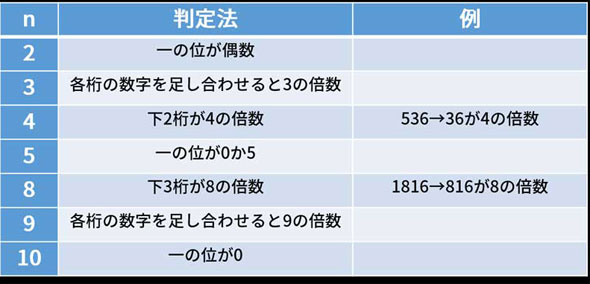
MathAquarium例題整数の性質 1 整数の性質 1 倍数の性質 a,b は整数とする。a+b,a が3 の倍数ならば,b は3 の倍数であることを証明せよ。 要点 整数a と0 でない整数b に対して, a=bk となる整数k があるとき,a はb の 倍数 であるという。 0 はすべての整数の倍数である。 末尾二桁が75であるため、4の倍数でないと判断できるのです。 とても簡単ですね! 4の倍数の判定方法の証明 それでは、この4の倍数の判定方法はなぜ成立するのかということについて、その証明も行っていきましょう。 ある5ケタの数(edcba)があるとし
数a 約数と倍数 証明
数a 約数と倍数 証明- 約数と倍数 小学生のときにも約数と倍数の話が出てきました。 なので、ほとんどがすでに知っている内容ですが、1つだけ大きな違いがあります。 それは、中学のときに、負の数を学んだ影響がある、という点です。 1,2,3,⋯ 1, 2, 3, ⋯ という数を、自然前回 https//googl/UwgSgk 次回 https//googl/9vCW59動画のプリント(19ch) http//www19chtv/サブチャンネル とある男が

整数 怜悧玲瓏 高校数学を天空から俯瞰する
(証明)「 3 ならば 4 」という命題とその対偶「 4 でない ならば 3 でない」という命題の真偽は一致する。 もとの命題の証明をしたいときに代わりに対偶を証明してもよい。この証明法を「対偶証明法」という。 ここで「対偶証明法」を用いる。倍数の証明のポイントは!・整数というグループを,示したい倍数の余りのグループに分けて考える!・連続した 3 つの整数の積は「 3 の倍数 文字設定 整数の証明では、式を立てて、計算することで問題文の内容が正しいことを示します。 その際 「 連続する二つの奇数」という 言葉のままでは計算も何もできないので、まずは言葉を文字式で表します。 そのことを文字設定と呼びます。 文字設定は自分で考えないといけない
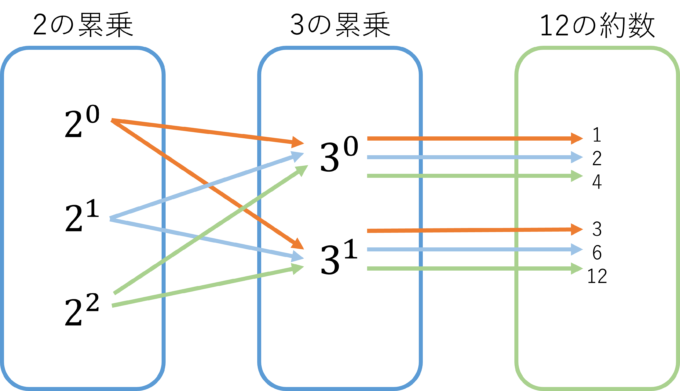
たとえば p = 113 は素数です。 113 の約数は 1 と 113 の 2 個です。 証明 p が素数であるとすると、素数の定義から p は 1 と p 以外の整数では割り切れません。 よって、 p の約数は 2 個です。 逆に 2 以上の整数 p は、かならず 1 と p で割り切れます。 よって、 p の約数が 2 個であるとき、 p が 11 倍数・約数 11 定理 11; 素数,合成数,素因数分解 定義 素数:2以上の自然数で,正の約数が1とその数自身のみである数 合成数:2以上の自然数で,素数でない数 因数:整数がいくつかの整数の積で表されるときのそれぞれの整数 素因数:素数である因数 素因数分解:自然数を素数だけの積の形に表すこと
数a 約数と倍数 証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「数a 約数と倍数 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「数a 約数と倍数 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「数a 約数と倍数 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「数a 約数と倍数 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「数a 約数と倍数 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「数a 約数と倍数 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
「数a 約数と倍数 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「数a 約数と倍数 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「数a 約数と倍数 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「数a 約数と倍数 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「数a 約数と倍数 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
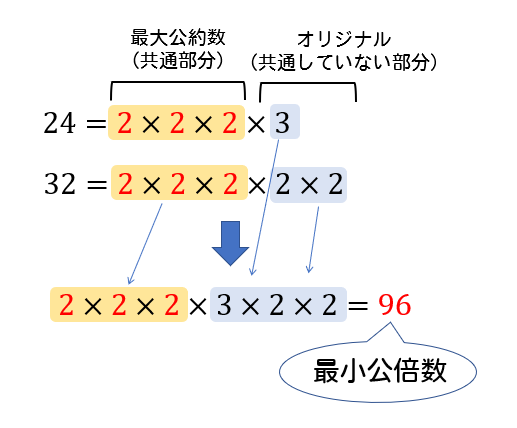
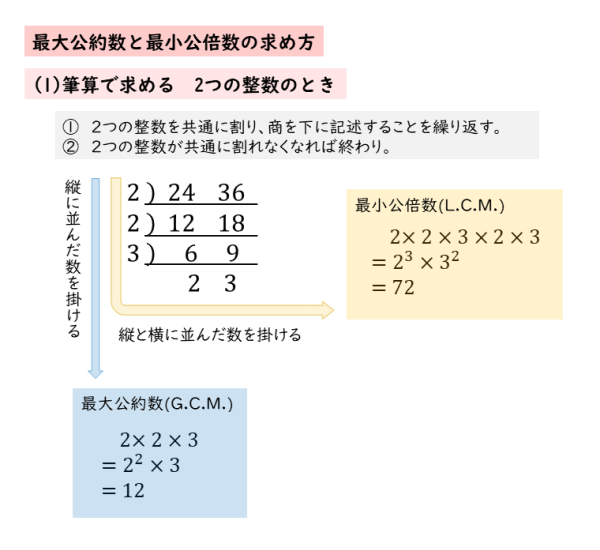
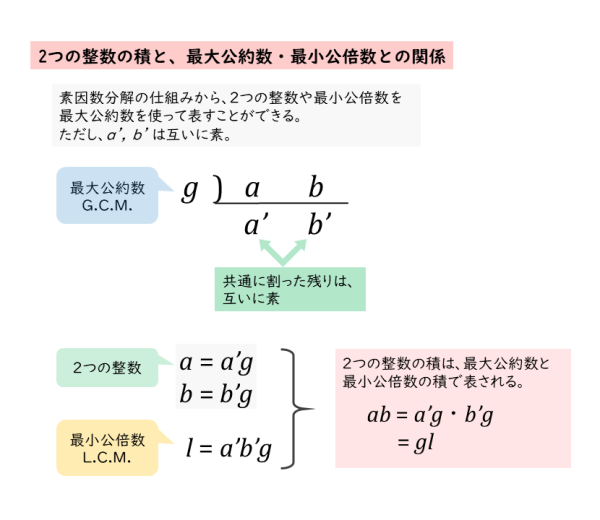
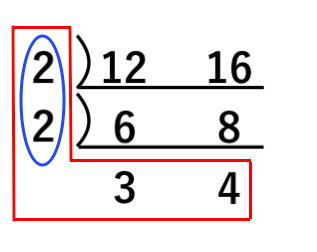
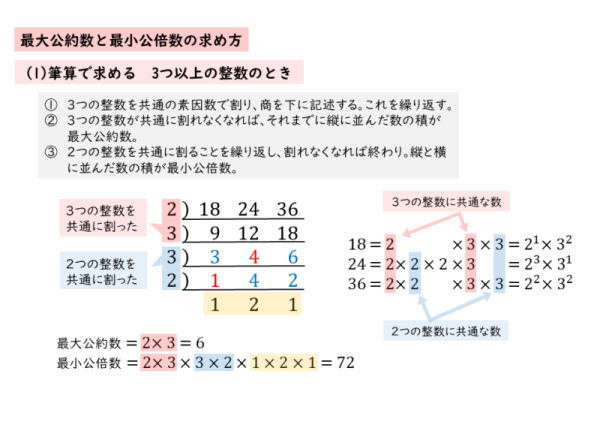
簡単に証明しておきます。 証明 連続する3つの整数のうち,1つは偶数で,1つは3の倍数であるから,連続する3つの整数の積は偶数かつ3の倍数,すなわち6の倍数である。 今回の問題では,まず因数分解すると次のようになります。 a,bの任意の公約数は最大公約数の約数である a, b の任意の公約数を d, 最大公約数を G とするとき l c m ( d, G) = G が成り立つことを示す. d, G の最小公倍数を l とすると l c m ( d, G) = l 公倍数の定義より G ≦ l d a かつ G a より a は d, G の公倍数. d, G の
Incoming Term: 約数と倍数 証明, 約数と倍数 証明問題, 数a 約数と倍数 証明,




0 件のコメント:
コメントを投稿